FocusonPCB - Vicenza, 15-16 maggio 2024
Torna a Vicenza il 15 e 16 maggio 2024 Focus on PCB, la terza edizione della fiera dedicata all'intera filiera dei circuiti stampati. Nata dalla volontà del Gruppo PCB Assodel…
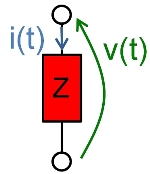
L’impedenza di un bipolo lineare rappresenta l'estensione del concetto di resistenza elettrica alle applicazioni in corrente alternata.
Più precisamente, rappresenta l’estensione al campo complesso (dominio dei fasori o di Laplace) del concetto di resistenza ed è definita come il rapporto tra la tensione sinusoidale applicata tra i morsetti del bipolo e la corrente che vi scorre.
Maggiore è l’impedenza, maggiore è l’ostruzione che il sistema oppone al passaggio della corrente.
Nell’ipotesi di linearità, la corrente possiede la stessa frequenza della tensione, ma viene alterata in ampiezza e fase, rendendo così l’impedenza una quantità complessa (vettoriale), dotata appunto di modulo e fase o, equivalentemente, di parte reale (detta resistenza) ed immaginaria (detta reattanza).
La parte reale è legata alla dissipazione di potenza, mentre la reattanza è legata all’immagazzinamento di energia nel bipolo. L’unità di misura dell’impedenza sono gli Ohm e il suo inverso (sempre complesso) è l’ammettenza (misurata in Siemens), la cui parte reale è la conduttanza e quella immaginaria è la suscettanza.
Poiché al variare della frequenza le proprietà del bipolo possono variare, l’impedenza è una grandezza complessa funzione della frequenza. La descrizione completa dell’impedenza di un bipolo è quindi data dai valori complessi dell’impedenza per tutto l’intervallo di frequenze di interesse, che ne costituiscono lo spettro.
Fig. 1 - Impedenza di un bipolo e sue rappresentazioni
La rappresentazione grafica dello spettro è comunemente offerta tramite il diagramma di Bode (grafici logaritimici separati del modulo e della fase al variare della frequenza – figura 1) ma esiste anche il diagramma di Cole-Cole, molto diffuso in ambito elettrochimico, che riporta in ascissa la parte reale e in ordinata l’opposto della parte immaginaria dell’impedenza per ogni punto tracciato per una frequenza diversa.
Oltre alla caratterizzazione delle proprietà dei componenti elettronici, la misura di impedenza trova impiego in numerosissimi ambiti, principalmente elettrochimici (dalle batterie alle vernici) e sensoristici (dai sensori di livello ai sensori MEMS), in quanto è un mezzo molto versatile per trasdurre variazioni di grandezze fisiche variegate in segnali elettrici.
Gli strumenti per la misura di impedenza (o LCR meter) si basano su tecniche differenti: analizziamo e confrontiamo quelle maggiormente adottate.
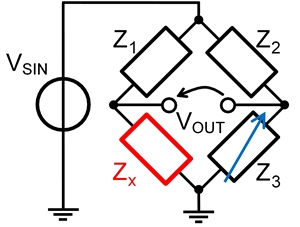Fig. 2 - Ponte di Wheatstone per la misura dell’impedenza ZxL’approccio più tradizionale è quello del ponte di Wheatstone. In questo caso (figura 2) il bipolo viene inserito in una struttura simmetrica costituita da due partitori realizzati con impedenze note Z1, Z2 e Z3.
Il ponte è alimentato con una tensione sinusoidale VSIN e si misura la caduta di tensione tra i due nodi centrali. I valori delle impedenze vengono variati (manualmente o automaticamente) fino a raggiungere la condizione di bilanciamento del ponte (detta null) nella quale la caduta di tensione differenziale è nulla e si può quindi ricavare il valore dell’impedenza incognita ZX = Z3·Z1/Z2.
I pregi di questa tecnica sono la reiezione dei disturbi di modo comune ed il fatto che l’amplificatore differenziale che legge la tensione di uscita operi sempre attorno a zero. L’accuratezza della misura non dipende criticamente dai circuiti di lettura, bensì dall’accuratezza degli altri elementi del ponte.
Fig. 3 - Ponte di impedenza manuale I difetti principali sono l’elevato numero di commutatori presenti, la necessità di conoscere a priori il tipo di impedenza (scegliendo tra un limitato numero di modelli equivalenti come combinazioni di resistenze e capacità o induttanze in serie o in parallelo) e la scomodità della routine di bilanciamento. Questi strumenti non si adattano quindi a misure di spettroscopia di impedenza.
A scopo didattico è mostrato in figura 3 uno storico strumento a ponte della General Radio (modello GR-1650B) in cui è visibile al centro l’indicatore a lancetta del bilanciamento, in alto a sinistra la manopola di selezione del modello equivalente (CS, CP, R, L…) ed in basso la regolazione fine del valore.
Fig. 4 - Capacimetro a ponte ad altissima risoluzione Esistono comunque degli strumenti moderni (e automatici) basati sulla configurazione a ponte, tra cui i capacimetri della Andeen-Hagerling. Questi ponti capacitivi che operano su una trentina di frequenze fisse da 50 Hz a 20 kHz (come il modello AH2700A mostrato in figura 4) rappresentano i capacimetri da banco con uscita digitale tra i più sensibili presenti su mercato, possedendo una risoluzione estrema inferiore all’attoFarad (10-18 F) raggiungibile a 1 kHz applicando alcuni volt di tensione e con un’accuratezza dichiarata di 5 ppm.
Una versione semplificata del ponte è la configurazione raziometrica, corrispondente a mezzo ponte, ovvero ad un semplice partitore in corrente alternata. La misura ottimale si ottiene quando il valore dell’impedenza nota Z1 posta in serie è prossima al valore dell’impedenza da misurare ZX.
Infatti, se Z1 >> ZX la tensione di uscita del partitore sarà prossima a zero, mentre se Z1 << ZX, la tensione di uscita sarà prossima a VSIN, diventando meno sensibile al valore di ZX. Oltre alla semplicità di realizzazione, il vantaggio principale di questo schema è che l’impedenza incognita ZX può avere un morsetto vincolato a massa.
Lo svantaggio è che eventuali elementi parassiti verso massa (resisitivi o capacitivi) afferenti al nodo VOUT si trovano direttamente in parallelo a ZX, alterandone l’accuratezza (e limitando la banda di misura).
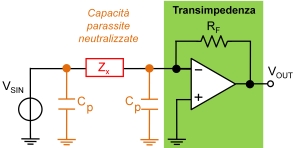Fig. 5 - Schema di misura con lettura della corrente tramite front-end a transimpedenzaLa configurazione più versatile e generamente migliore dal punto di vista della sensibilità è quella a lettura di corrente tramite amplificatore a transimpedenza (figura 5).
In questo caso è necessario avere accesso ad entrambi i morsetti dei bipolo di cui si vuole misurare l’impedenza, che non è possibile mantenere collegato a massa. Un morsetto viene collegato ad un generatore di tensione sinusoidale mentre l’altro morsetto è collegato all’ingresso a bassa impedenza di un lettore di corrente (ovvero alla terra virtuale di un amplificatore a transimpedenza). Quest’ultimo converte la corrente che scorre in ZX in una tensione di uscita proporzionale alla corrente, e quindi all’ammettenza incognita.
Il valore della resistenza di feedback RF (1 kΩ – 100 kΩ) può essere variato tramite un selettore interno, in modo da adattare il guadagno ai diversi intervalli di correnti corrispondenti a diverse decadi di valori di impedenza.
Il segnale di uscita può essere quindi raddrizzato per ottenere il modulo dell’ammettenza o demodulato con un demodulatore sincrono (tipo lock-in) che permette di ottenere separatamente le componenti in fase ed in quadratura dell’impedenza (necessarie per la completa caratterizzazione del modulo e della fase dello spettro di impedenza).
Fig. 6 - LCR meter di precisione da banco La maggior parte degli strumenti professionali di misura di impedenza si basa su questa architettura, in particolare gli strumenti prodotti da Agilent. Tra essi va certamente menzionato il modello E4980A (figura 6), un LCR meter di precisione funzionante da 20 Hz a 2 MHz che personalmente ritengo molto valido sia in termini di risoluzione che di robustezza.
L’unico piccolo difetto che si manifesta nel suo utilizzo è la scarsa intuitività della navigazione nei menù interni (in particolare per il salvataggio su file dei dati memorizzati in tabella). Lo stato dell’arte in questa gamma di frequenze è rappresentato dall’ottimo impedance analyzer modello 4294A (purtroppo con salvataggio dati ancora sugli obsoleti floppy disk) che funziona da 40 Hz fino a 110 MHz. Mentre il modello 4991A RF opera da 1 MHz a 3 GHz.
Le tecniche risonanti permettono la misura di una piccola variazione (tipicamente fino a qualche ppm) di impedenza convertendola in una variazione della frequenza di risonanza di un circuito risonante in cui viene inserita l’impedenza incognita.
Sebbene queste tecniche permettano di raggiungere sensibilità molto elevate anche con un front-end semplificato (ad esempio zero-cross detector/timer implementati con microcontrollori), sono adatte ad impedenze puramente reattive (prive di parassitismi resistivi significativi).
Inoltre sono generalmente sconsigliate in contesti di misura general purpose in quanto possono richiedere frequenze di lavoro molto elevate (GHz) e sono inadatte alla misura del valore assoluto dell’impedenza, di cui è necessario conoscere a priori la natura (capacitiva o induttiva).
Esistono infine tecniche di misura basate sulla trasformata di Fourier. In questo caso, l’impedenza incognita viene stimolata con una forma d’onda arbitraria, non necessariamente sinusoidale, ed il corrispondente segnale di corrente viene campionato ed acquisito direttamente. Poi in ambito digitale viene eseguita la FFT per ricavarne lo spettro.
Il vantaggio di questo approccio è che, potendo sovrapporre contemporaneamente più componenti spettrali, il tempo di misura necessario ad eseguire uno spettro è minore rispetto agli approcci precedenti, a fronte di un maggiore peso computazionale per la sezione di elaborazione numerica e della necessità di disporre di un generatore di forme d’onda arbitrarie operante a larga banda.
A pari potenza rms applicata al dispositivo, il rapporto segnale/rumore è inferiore. in quanto la potenza non è più concentrata ad una singola armonica, ma viene distribuita tra varie componenti spettrali.
In generale l’intervallo di impedenze misurabili dalla maggior parte degli strumenti va dall’Ohm alle decine/centinaia di MOhm.
Infatti, dal punto di vista strumentale è difficile misurare sia impedenze molto elevate (GOhm), in quanto la corrente è corrispondemente piccola e difficilmente discriminabile in presenza di rumore, sia impedenze molto piccole (frazioni di Ohm) in quanto i parassitismi del setup (come la resistenza serie dei collegamenti) giocano un ruolo non più trascurabile (richiedendo ad esempio un’approccio di misura a 4 terminali).
La corretta interpretazione dei valori di impedenza misurati richiede particolare attenzione. Prima di tutto vanno sempre tenuti in conto gli elementi parassiti che inevitabilmente affliggono la configurazione di misura ed il dispositivo stesso.
Gli strumenti più completi consentono di eseguire una calibrazione preliminare per compensare internamente gli errori dovuti alla configurazione del banco di misura (in particolare all’impedenza di accoppiamento tra i cavi di collegamento e delle fixture impiegate) con semplici procedure di misura con morsetti flottanti (open) e cortocircuitati (short) o fornendo anche campioni calibrati.
Inoltre, l’impedenza del dispositivo in esame va correttamente modellizzata. Ad esempio i resistori SMD possiedono una capacità parassita in parallelo di circa 0,2 pF, mentre i condensatori si comportano come tali solo a basse frequenze, fino alla frequenza di autorisonanza (10 Hz - 10 kHz), oltre la quale prevale il comportamento induttivo dovuto all’induttanza serie parassita dei terminali di collegamento.
Da ultimo, sebbene si utilizzi la modalità di auto range degli strumenti per evitare la saturazione, l’ampiezza del segnale applicato al dispositivo va scelta in modo da garantire sempre la permanenza in condizioni di linearità (tipicamente da qualche mV a qualche V a seconda del dispositivo) del circuito di misura interno dello strumento.
