Gli oscilloscopi sono sul mercato da molto tempo e i lettori meno giovani ricorderanno con una buona dose di nostalgia i bei tempi andati dei gloriosi “cassoni” analogici degli anni ’60 e ’70.

Molti strumenti analogici sono sopravvissuti e sono tuttora utilizzabili, soprattutto se non si ha bisogno di grandi larghezze di banda (e se si ha la possibilità di calibrarli adeguatamente al bisogno). Molti tecnici e ingegneri si sono fatti le ossa con quei colossi e si ha anche la possibilità di imparare ancora molto se si osa dare un’occhiata al loro interno.

Vediamo come si sono evolute nel tempo le principali caratteristiche degli oscilloscopi, ormai diventati tutti strumenti digitali, in particolare larghezza di banda e risoluzione.

Da sempre il sacro Graal degli oscilloscopi è stata considerata la sua larghezza di banda.

Ad esempio, un tempo, per un semplice amatore, un oscilloscopio da 30 MHz era sufficiente a vedere l’emissione fondamentale di un trasmettitore a onde corte (quindi sotto i 30 MHz); presto però le larghezze di banda cominciarono ad aumentare fin verso i 100 MHz, così da permettere di apprezzare oltre alla fondamentale, anche la terza, quarta e magari anche la quinta armonica. Un vero lusso!

Da allora gli oscilloscopi analogici hanno cominciato a ceder il passo agli strumenti digitali: se un hobbysta può ancora oggi accontentarsi di uno strumento con una larghezza di banda di 100 MHz, i professionisti hanno tipicamente di strumenti con una larghezza di banda di diversi ordini di grandezza superiore per svolgere efficacemente le loro attività quotidiane.

La buona notizia è che oggi sul mercato c'è l'imbarazzo della scelta e si possono scegliere strumenti che arrivano a catturare segnali anche dell'ordine dei gigahertz e delle decine di gigahertz, persino di 100 GHz, come ad esempio l'oscilloscopio LabMaster 10 Zi-A di Teledyne LeCroy, uno strumento capace di acquisire i segnali con frequenze di campionamento fino a 240 GS/s.

Per gli oscilloscopi digitali la larghezza di banda è tuttora fondamentale, ma non esaurisce tutte le caratteristiche salienti della macchina. Ad esempio, con tutta la potenza di calcolo incorporata negli strumenti moderni, ci sono aspetti come le opzioni di trigger e le possibilità di effettuare misure standardizzate e automatica da considerare attentamente.

Ancora più importante è la risoluzione verticale.

Già i primi oscilloscopi digitali avevano introdotto un grosso miglioramento rispetti ai vecchi strumenti analogici in termini di accuratezza di misura delle ampiezze (asse verticale).

I primissimi oscilloscopi digitali introdotti sul mercato avevano front-end verticali basati su convertitori analogico-digitali (ADC) a 6 bit. Già pochi anni dopo furono introdotti oscilloscopi digitali con ADC a 8 bit, che tuttora sono quelli più diffusi sul mercato.

Per vedere le cose in prospettiva, va ricordato che un ADC 6 bit ha una risoluzione di 64 livelli discreti sull’asse verticale, mentre un ADC 8 bit ne ha 4 volte tanto, arrivando quindi a garantire una risoluzione di 256 livelli discreti (ci si riferisce al numero di livelli in cui l’ADC riesce a dividere l’ampiezza massima di segnale che riesce a quantizzare senza distorsione).

Per la maggior parte delle applicazioni di elettronica generale, una risoluzione verticale di 8 bit è sufficiente, ed è così da decenni ormai. Tuttavia, come miglioramento 'ad interim', diversi costruttori hanno cercato di migliorare la risoluzione verticale, a parità di hardware di conversione ADC a 8 bit, con alcuni artifici a livello software, come medie su acquisizioni multiple e vari modi di cosiddette e non meglio specificate “risoluzioni aumentate” o “alte risoluzioni”.

Queste tecniche hanno la loro ragion d'essere, ma introducono anche delle limitazioni (ed esempio, funzionano bene spesso solo fino a una frequenza di lavoro inferiore a quella massima dello strumento).

Nel frattempo, la tecnologia degli ADC è migliorata notevolmente e alcuni costruttori, come Teledyne LeCroy, oltre un decennio fa già iniziarono a commercializzare strumenti con un ADC a 12 bit, pur mantenendo l'elevata frequenza di campionamento necessaria per analizzare i segnali ad alta frequenza.

Ricordando la notazione binaria, sappiamo che un front end basato su un ADC a 12 bit equivale ad avere 4096 livelli discreti di quantizzazione verticale. Significa un miglioramento di 16 volte sullo standard offerto dagli oscilloscopi con ADC a 8 bit. Oggi questa tipologia di strumenti viene comunemente indicata con il nome di oscilloscopio ad alta definizione o oscilloscopio HD.

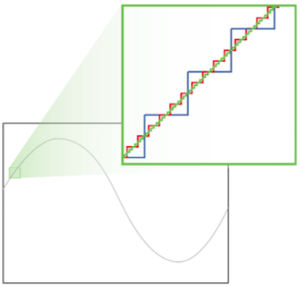 Differenza dei passi di quantizzazione tra ADC con diversa risoluzione verticale (8 bit in blu, 10 bit in rosso e 12 bit in verde)Cosa comporta in pratica per l’utente? Sostanzialmente essere in grado di vedere dettagli molto più fini sul segnale: ad esempio, la figura rappresenta la quantizzazione a 8 bit, 10 bit e 12 bit (traccia blu, rossa e verde nel riquadro) di una forma d’onda analogica.

L’inserto nella figura rappresenta è un ingrandimento della porzione di una forma d’onda sinusoidale, ideale e senza rumore. Possiamo vedere l’errore causato dal campionamento di questa forma d’onda causato dagli ADC con differenti risoluzioni.

A questo livello di ingrandimento il convertitore a 8 bit produce errori di quantizzazione molto evidenti, che invece si riducono a livelli appena percettibili nel caso del convertitore a 12 bit. È importante ribadire che questo è un caso ideale di una forma d’onda senza rumore e che l’ingrandimento mostra il rumore di quantizzazione introdotto dal convertitore analogico/digitale in funzione del numero di bit di risoluzione.

Visivamente si nota la grande differenza che fanno 4 bit in più di risoluzione del convertitore!

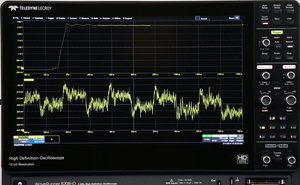Un oscilloscopio HD permette di osservare notidamente anche piccole variazione di segnale (finestra inferiore) sovrapposte a un segnale di maggiore ampiezza variabile lentamente (finestra superiore)All'atto pratico, un oscilloscopio ad alta definizione risulta particolarmente utile quando si devo osservare i dettagli di piccole variazioni di segnale piuttosto veloci sovrapposte a segnali di ampiezza molte maggiore variabili più lentamente.

Un primo caso di esempio è un segnale ampio sinusoidale su cui è sovrapposto un segnale parassita (o al limite anche solo rumore) molto più debole. In questo caso, se amplificassimo nello stadio d'ingresso dell'oscilloscopio il segnale ampio, perderemmo il segnale debole nel rumore di quantizzazione del convertitore quando la risoluzione è troppo bassa. Si tratta sostanzialmente del caso illustrato dalla figura 2 nel caso ci sia un segnale debole che risulta sotto la soglia del rumore di quantizzazione. Un oscilloscopio a più alta risoluzione permetterebbe di vedere anche il segnale debole.

Un secondo caso è rappresentato di un ampio segnale sinusoidale che abbia una minima distorsione armonica. Anche in questo caso la presenza delle armoniche superiori si perderebbe nel rumore di fondo del convertitore quando la risoluzione è bassa, mentre potrebbe essere osservata (e misurata) con oscilloscopio ad alta risoluzione.

Questo secondo caso è meglio visualizzabile nel dominio delle frequenze, passando quindi a una visualizzazione dello spettro del segnale (nel caso di strumenti mixed domain con funzione FFT integrata) oppure calcolando offline la trasformata di Fourier del segnale acquisito (ad esempio su un PC collegato all’oscilloscopio).

la risoluzione del convertitore si manifesta in un diverso livello del rumore di fondo dello spettro, che risulta più basso nel caso di strumenti ad alta risoluzione verticale, permettendo così ai picchi di eventuali armoniche di “sbucare” al di sopra del livello di rumore di fondo.

Ricordando che, su tutta la prima zona di Nyquist, il rapporto segnale-rumore di un segnale sinusoidale con ampiezza pari al fondo scala campionato da un ADC a N bit è dato da SNR (dB)=6.02*N+1.76, si vede che un incremento di 4 bit di risoluzione equivale un abbassamento di 24 dB del livello di rumore di fondo (a parità di frequenza di campionamento e numero di punti acquisiti), con tutti i vantaggi che ne derivano in termini di rilevazione di armoniche deboli.